최소신장트리(Minimum Spanning Tree, MST)는 연결 그래프에서 모든 노드를 연결하는 트리(Tree)를 만들 때, 간선의 가중치 합이 최소가 되도록 하는 사이클이 존재하지 않는 트리를 말합니다. 이는 그래프 이론에서 매우 중요한 문제 중 하나이며, 실제로 최소신장트리 알고리즘은 다양한 분야에서 활용되고 있습니다.
대표적인 최소신장트리 알고리즘으로는 Kruskal 알고리즘과 Prim 알고리즘이 있습니다. Kruskal 알고리즘은 그리디 알고리즘(Greedy Algorithm)을 기반으로 하며, 간선의 가중치가 작은 순서대로 간선을 선택하여 트리를 만들어 나가는 방식입니다. 반면, Prim 알고리즘은 시작점에서부터 출발하여 연결된 노드들 중에서 가장 가중치가 작은 간선을 선택하여 트리를 만들어 나가는 방식입니다.
최소신장트리 문제는 네트워크 설계, 도로 건설, 전기 회로 설계 등 다양한 분야에서 활용되고 있으며, 크루스칼 알고리즘과 프림 알고리즘이 모두 효과적인 알고리즘이며, 이 중에서도 각각의 특성에 따라 알고리즘을 선택하여 적용하는 것이 중요합니다.
1. 크루스칼 알고리즘
크루스칼 알고리즘은 그리디(Greedy) 알고리즘을 기반으로 하며, 간선의 가중치를 기준으로 정렬한 뒤에 가장 작은 가중치를 가진 간선부터 하나씩 선택하여 최소신장트리를 만들어 나가는 방식입니다.
구체적인 동작 방식은 다음과 같습니다.
1) 모든 간선을 가중치를 기준으로 정렬합니다.
2) 가장 작은 가중치를 가진 간선부터 선택하여 트리에 추가합니다.
3) 이전에 추가된 간선과 이번에 선택된 간선이 서로 다른 그래프를 이루고 있다면, 두 그래프를 연결하는 간선으로 추가합니다.
4) 모든 노드가 포함될 때까지 2-3번의 과정을 반복합니다.
크루스칼 알고리즘의 시간 복잡도는 O(ElogE)입니다. E는 간선의 수를 의미합니다.
간단하게 말하자면, 그래프 간선들을 가중치의 오름차순으로 정렬해 놓은 뒤, 사이클을 형성하지 않는 선에서 정렬된 순서대로 간선을 선택한다.
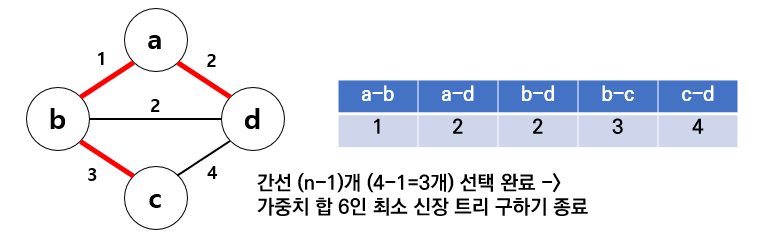
[1] 그래프 간선을 가중치 오름차순 정렬합니다.

[2] a-b 부터 선택합니다.

[3] 그 다음 a-d를 선택합니다.

[4] 그 다음 b-d를 선택하면 a-b-d 사이클이 형성되므로 선택하지 않습니다.

[5] 그 다음 b-c를 선택합니다. 선택된 간선의 갯수가, 정점의 갯수-1 만큼 되면 종료합니다.
사이클 판단하기 - Union & Find 활용
위에서 [4]번 과정에서 싸이클 판별하여 넘어 갔었는데, 이것을 구현할 때는 Union&Find 메소드를 사용한다.
- Union-Find 란?
- Disjoint Set (서로소 집합) 을 표현하는 자료구조
- 서로 다른 두 집합을 병합하는 Union 연산, 집합 원소가 어떤 집합에 속해있는지 찾는 Find 연산을 지원하기에 이러한 이름이 붙었음

간선 선택 전, 1번~4번 노드는 초기에 각각 서로소 집합 {1}, {2}, {3}, {4}로 표현될 수 있습니다.
- parent 배열은 각 정점의 root node(부모)를 표현한 배열
- 초기에는 자기 자신이 루트 노드가 되게 초기화 되어 있는 상태 (parent[i] = i)
가중치의 오름차순 정렬한 순서대로 간선 1-2 를 선택합니다.
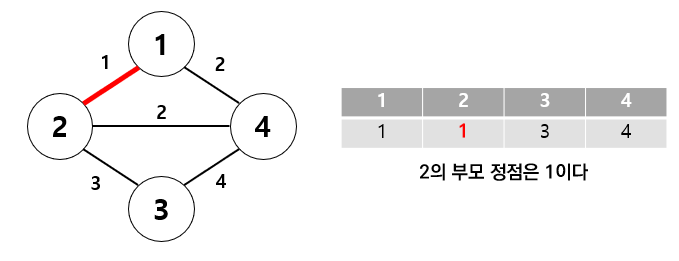
이 때, 1번과 2번이 같은 집합으로 Union 연산에 의해 합쳐진 것입니다. 그리고 2번의 부모는 1번이 됩니다.
다음으로 간선 1-4를 선택합니다.

1과 4를 연결해야 합니다. 1의 루트 노드는 1이고, 4의 루트 노드는 4 이므로 서로 다른 부모를 가집니다.
따라서 Union 연산으로 합칠 수 있으며, 합친 결과 {1, 2, 4} 집합이 되었습니다.
그리고 {1, 2, 4} 집합에서 루트 노드는 1 입니다. 즉, 2번의 부모는 1번이고, 4번의 부모도 1번입니다.
다음으로 weight가 가장 작은 간선 2-4를 선택합니다.

2와 4를 연결해야 합니다. 그런데, 2의 루트 노드는 1이고, 4의 루트 노드도 1 입니다.
(parent[2] = 1, parent[4] = 1 –> parent[2] == parent[4])
이미 서로 부모가 같기 때문에 Union 연산을 하지 않습니다. 만약 합친다면 위 그래프처럼 사이클을 형성하게 되기 때문입니다.
Union과 Find 메소드 구현
public static void union(int a, int b) {
int aP = find(a);
int bP = find(b);
if (aP != bP) {
parents[aP] = bP;
}
}
public static int find(int a) {
if (a == parents[a]) {
return a;
}
return parents[a] = find(parents[a]);
} if (find(data[i][0]) != find(data[i][1])) {
union(data[i][0], data[i][1]);
weightSum += data[i][2];
}위 코드는 크루스칼 함수의 중요 로직으로 node1(data[i][0]) 에서 node2(data[i][1])로 서로의 parents가 같지 않으면 서로 union으로 연결하고, weight를 더해줘서 최소신장트리의 값을 구해준다.
2. 프림 알고리즘
프림 알고리즘은 시작점에서부터 출발하여, 현재 트리와 연결된 노드들 중에서 가장 작은 가중치를 가진 간선을 선택하여 최소신장트리를 만들어 나가는 방식입니다.
구체적인 동작 방식은 다음과 같습니다.
1) 시작점을 선택하여 트리에 추가합니다.
2) 현재 트리와 연결된 노드들 중에서 가장 작은 가중치를 가진 간선을 선택하여 트리에 추가합니다.
3) 2번의 과정에서 추가된 노드와 연결된 간선들 중에서, 트리에 이미 추가된 노드와 연결된 간선은 제외하고 가장 작은 가중치를 가진 간선을 선택하여 트리에 추가합니다.
4) 모든 노드가 포함될 때까지 2-3번의 과정을 반복합니다.
프림 알고리즘의 시간 복잡도는 O(ElogV)입니다. E는 간선의 수, V는 노드의 수를 의미합니다.

위 그래프의 최소 신장 트리를 프림 알고리즘으로 구해보자. 시작 정점은 아무 노드를 넣어도 되지만 A로 한다.

A와 인접한 노드 B, C 중 C가 가장 가중치가 낮은 간선으로 연결되어 있으니 C를 집합에 넣고 비용에 AC 가중치를 더한다.

AC와 인접한 노드들 중 가장 낮은 가중치(2,3,4,6 중 2)로 연결된 정점은 B다. 집합에 B를 넣고 CB 가중치를 더한다.

A, C, B와 인접한 노드들 중 가장 낮은 가중치(3,4,5,6 중 3)로 연결된 정점은 D다. 집합에 D를 넣고 CD 가중치를 더한다.

A, C, B, D와 인접한 노드들 중 가장 낮은 가중치(2,4,5,6 중 2)로 연결된 정점은 E다. 집합에 E를 넣고 DE 가중치를 더한다.

A, C, B, D, E와 인접한 노드들 중 가장 낮은 가중치(3,4,5,5,6 중 3)로 연결된 정점 F를 집합에 넣고 DF 가중치를 더한다. 트리의 집합에 속한 원소의 개수가 N이 되었으므로 탐색을 중단한다. 탐색 결과 최소 신장 트리 구축의 비용은 13으로 확인되었다.
프림 알고리즘 구현
프림 알고리즘은 우선순위 큐를 사용하면 O(ElogV)로 구현할 수 있다.
boolean[] visited = new boolean[v + 1];
PriorityQueue<Node> pq = new PriorityQueue<>((x, y) -> x.weight - y.weight);
pq.add(new Node(1, 0));
int cnt = 0;
while (!pq.isEmpty()) {
Node cur = pq.poll();
cnt+=1;
if (visited[cur.to]) {
continue;
}
visited[cur.to] = true;
weightSum += cur.weight;
if (cnt == v) {
return weightSum;
}
for (int i = 0; i < graph.get(cur.to).size(); i++) {
Node adjNode = graph.get(cur.to).get(i);
if (visited[adjNode.to]) {
continue;
}
pq.offer(adjNode);
}
}위 코드는 프림 알고리즘을 우선 순위 큐로 구현할 때의 핵심 로직을 담고 있다. ArrayList로 선언된 graph에 인접 노드에 방문 여부를 확인하고 방문하지 않았을 때 인접 노드로 갈 수 있는 간선들의 weight가 낮은 값부터 꺼내면서 weight에 더해준다.
출처 :
1) https://chanhuiseok.github.io/posts/algo-33/
2) https://8iggy.tistory.com/159
'Java' 카테고리의 다른 글
| [Java] Collection Set 정리하기 (0) | 2023.03.29 |
|---|---|
| [Java] 03/28 알고리즘 문제 (0) | 2023.03.29 |
| [프로그래머스] 03/24 문제 풀기 (0) | 2023.03.24 |
| 프로그래머스 : 이상한 문자 만들기 (0) | 2023.03.23 |
| 최단 경로 알고리즘 (0) | 2023.03.23 |